Rotating elements in Processing
Introduction
In Processing it is easily possible to transform graphical elements such as ellipses, or rectangles, but also images, text, or any other more complex objects. This tutorial gives an overview on how to rotate visual elements in different ways, and explains the mechanisms behind it.
Rotation
Turning elements around specific points, like the corner or the center of a visual object, can be achieved by calculating rotated points by trigonometric functions.
Luckily, Processing provides simple functions to rotate elements.
The following example visualizes one or multiple rotated rectangles:

Fig. 1: one rotated rectangle

Fig. 2: multiple rotated rectangles
The Processing code for Fig. 2:
rotate()
rotate(angle);
Rotates the drawing area (the coordinate system) with the given angle in units of radians. As it is clearly recognizable in Fig. 2 consider that …
- all elements are rotated around the point of origin (0, 0)
- multiple
rotate()-statements sum up.
Positive angle values rotate the elements clockwise, while negative values rotate them counter-clockwise.

Fig. 3: rotate(+45°)

Fig. 4: rotate(-45°)
In Processing – as in other screen based computer programs – the y-axis in the coordinate system is turned upside down, and so are the angle values. They go the other way around.
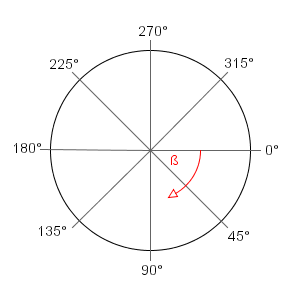
Fig. 5: Unit-circle with angles in degrees
Radians and degrees
The angle for the rotate() function has to be given in radians.
Thus, all of the three following code snippets result in the same rotation:
In the third example the angle is given in units of somewhat more intuitive, or more internalized degrees.
For this we can use the conversion function radians() – to convert a radians value in degrees use degrees().
Translation
If you want to rotate the elements not around the point of origin (upper left corner of the drawing area), but for instance
around their own origin, you can combine translate() with other transformations.
translate()
translate(x, y);
Moves the origin of the coordinate system to the given position. For instance, with a translation with an x-offset of 100 and a y-offset of 30 a point at position (50, 20) will be drawn at (150, 50).

Fig. 6: Without translation

Fig. 7: With translation
Translate calls are additive (as the rotate() function), i.e. if translate(10, 15) is run twice, the overall
offset would be (20, 30).
rotate() & translate()
Of course, the image of Fig. 7 could be achieved by directly drawing the rectangle at that position
(i.e. by executing rect(50, 50, 100, 100);). The problem herein is this would
not work as excepted, if additionally the element is rotated (see Fig. 9).

Fig. 8: rect(50, 50, 100, 100);

Fig. 9: "wrong" rotation around the point of origin of the drawing area
To get the correct result (i.e. a rotation around the visual point of origin of the rectangle),
translate() and rotate() have to be combined as in the following example. Note, that the rectangle
function now is called with position parameters of (0, 0), but after a translation of the origin with (50, 50) it is displayed
at and rotated around that new point.

Fig. 10: proper rotation about the upper left corner of the rectangle
Loops & animation
Quite interesting and nice results can be achieved, by utilizing multiple graphic transformations in a loop.
Loops
Follow the step-by-step process on how to create a spiral with the help of one for-loop and a simple rotation.






Animations
Of course, these transformations can be used and manipulated over time. For instance the angle could be varied, and used in an animation or be dependent from some user interaction.
Example: SquareFlower
Very simple interactive flower, made out of rotated squares.
- SquareFlower (Processing sketch)
- SquareFlower.pde (source), SquareFlower.zip (complete sketch archive)
Matrix
To rotate multiple elements in different, independent ways, matrices has to be used. Isolating transformations to just some elements is possible by employing an own matrix for those. Each transformation matrix stores stated rotations and translations and affects only elements drawn in that matrix.


The screenshots above show both rectangles with different rotations. In this RotateMultiElements example one rectangle is rotated interactively by mouse position, while the other is turning automatically.
pushMatrix()
pushMatrix();
Pushs a new transformation matrix on the stack. All subsequent transformations only affect this matrix –
as long as until the next popMatrix().
popMatrix()
popMatrix();
Takes the last tranformation matrix of the stack, thus the previous is the affected one.
Using push and pop matrix
In the following example all three rectangle functions are called with same x-parameter, but displayed at different horizontal positions.


The top rectangle is at its original position. The middle one is translated with (50, 0) twice, so its displayed position is at (100, 74).
The bottom one is translated once, because the second translation in line 6 was stated in another matrix,
which is not valid for the third rectangle anymore, due to the popMatrix().
Example: A clock
Shows the time on an analog clock. The three arrows – of course – rotate independently.

Example: FeedVisRadialThumbnails
Displays the image thumbnail of news feed items in a radial layout. The user can rotate and scale the image wheel with the mouse, interactively.


- FeedVisRadialThumbnails.pde (source), FeedVisRadialThumbnails.zip (complete sketch archive)
- See also the Processing RSS Feeds tutorial.